Constructing VLE Diagrams using Equation of State Methods

Contents

Constructing VLE Diagrams using Equation of State Methods#

Teng-Jui Lin

Content adapted from UW CHEME 326, Chemical Engineering Thermodynamics, in Winter 2022.

Problems reprinted from Koretsky, M. D. Engineering and Chemical Thermodynamics. (Wiley, 2012).

Comparison of vdW and Peng-Robinson EOS for predicting VLE behavior#

Koretsky Example 8.17. The following data are available for vapor–liquid equilibrium of the methane (1) n-pentane (2) binary system at 37.78°C. Compare how well the van der Waals and Peng–Robinson equations can represent these data using the equation of state method to calculate fugacity coefficients of the vapor and the liquid.

P_truth = np.array([13.82, 27.68, 41.45, 55.26, 69.08, 86.35, 103.62, 120.89, 138.16, 155.43, 172.70]) * 1e5 # bar to Pa
y1_truth = np.array([0.8954, 0.9322, 0.9422, 0.9486, 0.9494, 0.9483, 0.9421, 0.9296, 0.9128, 0.889, 0.849])
x1_truth = np.array([0.0646, 0.1293, 0.1892, 0.2453, 0.2965, 0.3565, 0.4152, 0.4782, 0.5509, 0.635, 0.735])

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.lines import Line2D
from scipy import optimize
from sympy import Symbol
from sympy.solvers import solve

# plot settings
%config InlineBackend.figure_format = 'retina'
%matplotlib inline

plt.rcParams.update(
    {
        "font.family": "Arial",  # Times New Roman, Calibri
        "font.weight": "normal",
        "mathtext.fontset": "cm",
        "font.size": 18,
        "lines.linewidth": 2,
        "axes.linewidth": 2,
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.titleweight": "bold",
        "axes.titlesize": 18,
        "axes.labelweight": "bold",
        "xtick.major.size": 8,
        "xtick.major.width": 2,
        "ytick.major.size": 8,
        "ytick.major.width": 2,
        "figure.dpi": 80,
        "legend.framealpha": 1,
        "legend.edgecolor": "black",
        "legend.fancybox": False,
        "legend.fontsize": 14,
    }
)

# given data
P_truth = np.array([13.82, 27.68, 41.45, 55.26, 69.08, 86.35, 103.62, 120.89, 138.16, 155.43, 172.70]) * 1e5 # bar to Pa
y1_truth = np.array([0.8954, 0.9322, 0.9422, 0.9486, 0.9494, 0.9483, 0.9421, 0.9296, 0.9128, 0.889, 0.849])
x1_truth = np.array([0.0646, 0.1293, 0.1892, 0.2453, 0.2965, 0.3565, 0.4152, 0.4782, 0.5509, 0.635, 0.735])

# liquid compositions to be simulated
x1_sim = np.arange(0.001, 1, 0.005)
x2_sim = 1 - x1_sim

vdW EOS#

# universal constant
R = 8.314  # J/mol K
# given properties
T = 37.78 + 273.15  # K

# formula for vdW params and saturation pressure
pure_a = lambda Tc, Pc, R: 27 / 64 * (R * Tc) ** 2 / Pc
pure_b = lambda Tc, Pc, R: 1 / 8 * (R * Tc) / Pc
antoine = lambda A, B, C, T: np.exp(A - B / (T + C)) * 1e5  # Pa

# physical properties - appendix a1
# methane (1)
A1 = 8.6041
B1 = 897.84
C1 = -7.16
Tc1 = 190.6  # K
Pc1 = 46.00e5  # Pa
a1 = pure_a(Tc1, Pc1, R)
b1 = pure_b(Tc1, Pc1, R)
# n-pentane (2)
A2 = 9.2131
B2 = 2477.07
C2 = -39.94
Tc2 = 469.6  # K
Pc2 = 33.74e5  # Pa
a2 = pure_a(Tc2, Pc2, R)
b2 = pure_b(Tc2, Pc2, R)
# mixture
a12 = np.sqrt(a1 * a2)

# saturation pressures
Psat1 = antoine(A1, B1, C1, T)
Psat2 = antoine(A2, B2, C2, T)

def solve_v(T, P, a, b, R, v_before, threshold=1e-10):
    """Solve vdW EOS for v."""
    coeff = [-a * b, a, -(R * T + P * b), P]
    # solve for compressibility factor
    v = np.polynomial.polynomial.polyroots(coeff)
    # z is real and positive
    v = np.real(v)
    v = v[v > 0]
    # double check if solution is good in case of algorithmic instability
    error = np.abs(np.polynomial.polynomial.polyval(v, coeff))
    v = v[error < threshold]
    # use the root closest to the last v
    closest_idx = np.argmin(np.abs(v - v_before))
    v = v[closest_idx]
    return v

# formula for mixed vdW params
mixed_a = (
    lambda comp1, comp2, a1, a2: comp1**2 * a1
    + 2 * comp1 * comp2 * np.sqrt(a1 * a2)
    + comp2**2 * a2
)
mixed_b = lambda comp1, comp2, b1, b2: comp1 * b1 + comp2 * b2

# formula for fugacity coefficients (phi_1, for phi_2, switch arguments of 1 and 2 properties)
phi = lambda comp1, comp2, P, v, T, R, a1, a12, b, b1: np.exp(
    b1 / (v - b)
    - np.log((v - b) * P / (R * T))
    - 2 * (comp1 * a1 + comp2 * a12) / (R * T * v)
)

vdw_a_v = []
vdw_b_v = []
vdw_P = []
vdw_y1 = []
vdw_y2 = []
vdw_v_v = []
vdw_v_l = []
vdw_phi_v1 = []
vdw_phi_v2 = []
vdw_phi_l1 = []
vdw_phi_l2 = []
v_v = 0
v_l = 0

for i in range(len(x1_sim)):
    # assign current liquid composition
    x1 = x1_sim[i]
    x2 = x2_sim[i]
    # estimate total pressure
    P = x1 * Psat1 + x2 * Psat2
    # estimate vapor compositions
    y1 = x1 * Psat1 / P
    y2 = x2 * Psat2 / P

    # iteratre through vdW EOS
    num_iter = 0
    max_iter = 10000
    tol = 0.001
    tol_criteria = tol * 2
    while tol_criteria > tol and num_iter < max_iter:
        # calculate vdW parameters for mixtures in each phase
        a_v = mixed_a(y1, y2, a1, a2)
        b_v = mixed_b(y1, y2, b1, b2)
        a_l = mixed_a(x1, x2, a1, a2)
        b_l = mixed_b(x1, x2, b1, b2)
        # solve vdW EOS for molar volume in each phase
        v_v = solve_v(T, P, a_v, b_v, R, v_before=v_v)
        v_l = solve_v(T, P, a_l, b_l, R, v_before=v_l)
        # print(i, num_iter, a_v, b_v, P)
        # print(i, num_iter, a_l, b_l, P)
        # print(i, num_iter, v_v, v_l)
        # calculate fugacity coefficient of each species in each phase
        phi_v1 = phi(y1, y2, P, v_v, T, R, a1, a12, b_v, b1)
        phi_v2 = phi(y2, y1, P, v_v, T, R, a2, a12, b_v, b2)
        phi_l1 = phi(x1, x2, P, v_l, T, R, a1, a12, b_l, b1)
        phi_l2 = phi(x2, x1, P, v_l, T, R, a2, a12, b_l, b2)
        # update vapor composition
        y1 = x1 * phi_l1 / phi_v1
        y2 = x2 * phi_l2 / phi_v2
        # update total pressure
        P = P * (y1 + y2)
        # calculate if calculation converges
        tol_criteria = abs(y1 + y2 - 1)
        num_iter += 1
    # store computed results
    vdw_a_v.append(a_v)
    vdw_b_v.append(b_v)
    vdw_v_v.append(v_v)
    vdw_v_l.append(v_l)
    vdw_phi_v1.append(phi_v1)
    vdw_phi_v2.append(phi_v2)
    vdw_phi_l1.append(phi_l1)
    vdw_phi_l2.append(phi_l2)
    vdw_y1.append(y1)
    vdw_y2.append(y2)
    vdw_P.append(P)

fig, ax = plt.subplots()

# plot raw data
ax.plot(x1_truth, P_truth, "kx")
ax.plot(y1_truth, P_truth, "ko", mfc="none")
# plot vdW simulated data
vdw_range_idx = 101
ax.plot(x1_sim[:vdw_range_idx], vdw_P[:vdw_range_idx], "k--")
ax.plot(vdw_y1[:vdw_range_idx], vdw_P[:vdw_range_idx], "k-")
ax.text(0.45, 0.3e7, "vdW EOS")
# plot settings
ax.set_xlim(0, 1)
ax.set_ylim(0, 200e5)
ax.set_xlabel("$x_1, y_1$")
ax.set_ylabel("$P$ (Pa)")
ax.set_title("Mix of Methane (1) and n-pentane (2) \n at T = 37.78°C")

# custom legend
legend_elements = [
    Line2D([0], [0], marker="x", ls="none", color="k", label="$x_1$ Data"),
    Line2D([0], [0], marker="o", ls="none", color="k", label="$y_1$ Data"),
    Line2D([0], [0], ls="--", color="k", label="$x_1$ EOS"),
    Line2D([0], [0], ls="-", color="k", label="$y_1$ EOS"),
]
ax.legend(handles=legend_elements, bbox_to_anchor=(1, 1))

<matplotlib.legend.Legend at 0x13b7dfd30>

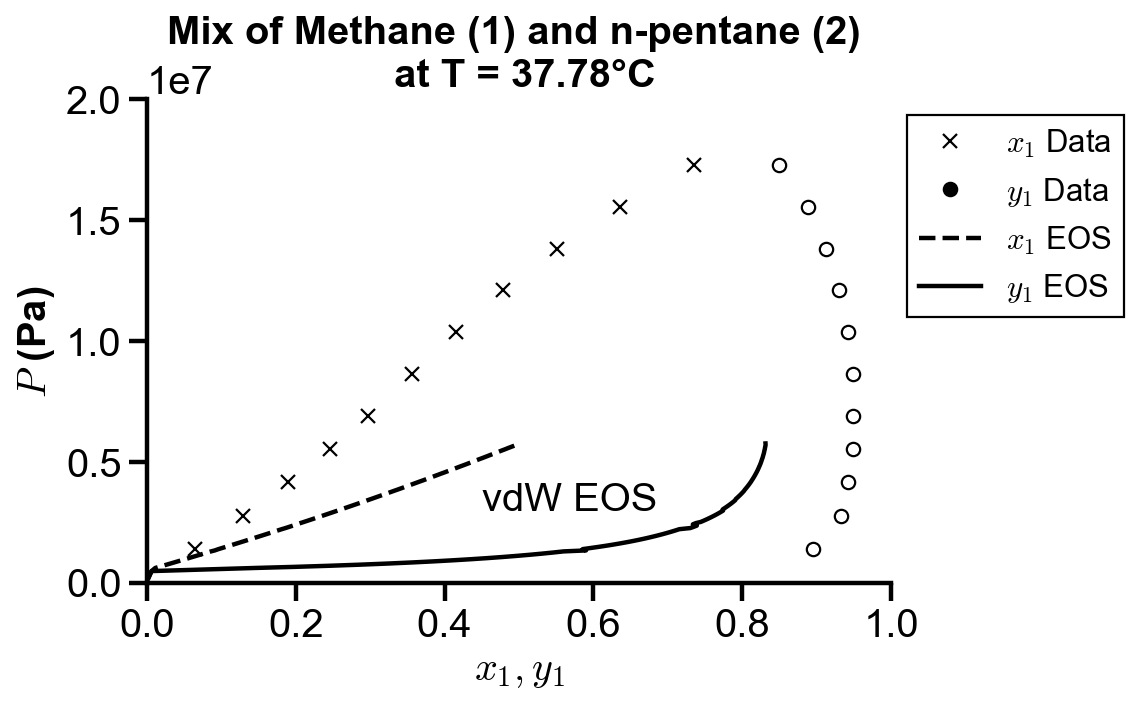
../../_images/6ae1bd0b878e3253e33ae40cd841a2efcd6e5bcf5e3fd5f5b38422a4cf674396.png

Peng-Robinson EOS#

# universal constant
R = 8.314  # J/mol K
# given properties
T = 37.78 + 273.15  # K

# formula for Peng-Robinson params and saturation pressure
pure_a = lambda Tc, Pc, R: 0.45724 * (R * Tc) ** 2 / Pc
pure_b = lambda Tc, Pc, R: 0.07780 * (R * Tc) / Pc
kappa = lambda omega: 0.37464 + 1.54226 * omega - 0.26992 * omega**2
alpha = lambda Tr, kappa: (1 + kappa * (1 - np.sqrt(Tr))) ** 2
antoine = lambda A, B, C, T: np.exp(A - B / (T + C)) * 1e5  # Pa

# physical properties - appendix a1
# methane (1)
A1 = 8.6041
B1 = 897.84
C1 = -7.16
omega1 = 0.008
Tc1 = 190.6  # K
Pc1 = 46.00e5  # Pa
Tr1 = T / Tc1
a1 = pure_a(Tc1, Pc1, R)
b1 = pure_b(Tc1, Pc1, R)
kappa1 = kappa(omega1)
alpha1 = alpha(Tr1, kappa1)
a_alpha_1 = a1 * alpha1
# n-pentane (2)
A2 = 9.2131
B2 = 2477.07
C2 = -39.94
omega2 = 0.251
Tc2 = 469.6  # K
Pc2 = 33.74e5  # Pa
Tr2 = T / Tc2
a2 = pure_a(Tc2, Pc2, R)
b2 = pure_b(Tc2, Pc2, R)
kappa2 = kappa(omega2)
alpha2 = alpha(Tr2, kappa2)
a_alpha_2 = a2 * alpha2
# mixture
k12 = 0
a12 = np.sqrt(a1 * a2)
a_alpha_12 = np.sqrt(a_alpha_1 * a_alpha_2)

# saturation pressures
Psat1 = antoine(A1, B1, C1, T)
Psat2 = antoine(A2, B2, C2, T)

def solve_v(T, P, a_alpha, b, R, v_before, threshold=1e-10):
    """Solve Peng-Robinson EOS for v."""
    A = a_alpha * P / (R * T) ** 2
    B = b * P / (R * T)
    coeff = [-(A * B - B**2 - B**3), A - 2 * B - 3 * B**2, -(1 - B), 1]
    # solve for compressibility factor
    z = np.polynomial.polynomial.polyroots(coeff)
    # z is real and positive
    z = np.real(z)
    z = z[z > 0]
    # double check if solution is good in case of algorithmic instability
    error = np.abs(np.polynomial.polynomial.polyval(z, coeff))
    z = z[error < threshold]
    # convert to v
    v = z * R * T / P
    v = v[v > b]
    # use the root closest to the last v
    closest_idx = np.argmin(np.abs(v - v_before))
    v = v[closest_idx]
    return v

# formula for mixed Peng-Robinson params
mixed_a_alpha = (
    lambda comp1, comp2, a_alpha_1, a_alpha_2, k12: comp1**2 * a_alpha_1
    + 2 * comp1 * comp2 * np.sqrt(a_alpha_1 * a_alpha_2) * (1 - k12)
    + comp2**2 * a_alpha_2
)
mixed_b = lambda comp1, comp2, b1, b2: comp1 * b1 + comp2 * b2

# formula for fugacity coefficients (phi_1, for phi_2, switch arguments of 1 and 2 properties)
phi = lambda comp1, comp2, P, v, T, R, a_alpha, a_alpha_1, a_alpha_12, b, b1: np.exp(
    b1 / b * (P * v / (R * T) - 1)
    - np.log((v - b) * P / (R * T))
    + a_alpha
    / (2 * np.sqrt(2) * b * R * T)
    * (b1 / b - 2 / a_alpha * (comp1 * a_alpha_1 + comp2 * a_alpha_12))
    * np.log((v + (1 + np.sqrt(2)) * b) / (v + (1 - np.sqrt(2)) * b))
)

# initialize guess
v_v = 0
v_l = 0
# generate lists to store iteration results
pr_a_alpha_v = []
pr_b_v = []
pr_P = []
pr_y1 = []
pr_y2 = []
pr_v_v = []
pr_v_l = []
pr_phi_v1 = []
pr_phi_v2 = []
pr_phi_l1 = []
pr_phi_l2 = []

for i in range(len(x1_sim)):
    # assign current liquid composition
    x1 = x1_sim[i]
    x2 = x2_sim[i]
    # estimate total pressure
    P = x1 * Psat1 + x2 * Psat2
    # estimate vapor compositions
    y1 = x1 * Psat1 / P
    y2 = x2 * Psat2 / P

    # iteratre through Peng-Robinson EOS
    num_iter = 0
    max_iter = 10000
    tol = 0.001
    tol_criteria = tol * 2
    while tol_criteria > tol and num_iter < max_iter:
        # calculate Peng-Robinson parameters for mixtures in each phase
        a_alpha_v = mixed_a_alpha(y1, y2, a_alpha_1, a_alpha_2, k12)
        b_v = mixed_b(y1, y2, b1, b2)
        a_alpha_l = mixed_a_alpha(x1, x2, a_alpha_1, a_alpha_2, k12)
        b_l = mixed_b(x1, x2, b1, b2)
        # solve Peng-Robinson EOS for molar volume in each phase
        v_v = solve_v(T, P, a_alpha_v, b_v, R, v_before=v_v)
        v_l = solve_v(T, P, a_alpha_l, b_l, R, v_before=v_l)
        # print(i, num_iter, v_v, v_l)
        # calculate fugacity coefficient of each species in each phase
        phi_v1 = phi(y1, y2, P, v_v, T, R, a_alpha_v, a_alpha_1, a_alpha_12, b_v, b1)
        phi_v2 = phi(y2, y1, P, v_v, T, R, a_alpha_v, a_alpha_2, a_alpha_12, b_v, b2)
        phi_l1 = phi(x1, x2, P, v_l, T, R, a_alpha_l, a_alpha_1, a_alpha_12, b_l, b1)
        phi_l2 = phi(x2, x1, P, v_l, T, R, a_alpha_l, a_alpha_2, a_alpha_12, b_l, b2)
        # update vapor composition
        y1 = x1 * phi_l1 / phi_v1
        y2 = x2 * phi_l2 / phi_v2
        # update total pressure
        P = P * (y1 + y2)
        # print(phi_v1, phi_v2, phi_l1, phi_l2)
        # print(y1, y2, P)
        # calculate if calculation converges
        tol_criteria = abs(y1 + y2 - 1)
        num_iter += 1
    # store computed results
    pr_a_alpha_v.append(a_alpha_v)
    pr_b_v.append(b_v)
    pr_v_v.append(v_v)
    pr_v_l.append(v_l)
    pr_phi_v1.append(phi_v1)
    pr_phi_v2.append(phi_v2)
    pr_phi_l1.append(phi_l1)
    pr_phi_l2.append(phi_l2)
    pr_y1.append(y1)
    pr_y2.append(y2)
    pr_P.append(P)

fig, ax = plt.subplots()

# plot raw data
ax.plot(x1_truth, P_truth, "kx")
ax.plot(y1_truth, P_truth, "ko", mfc="none")
# plot vdW simulated data
vdw_range_idx = 101
ax.plot(x1_sim[:vdw_range_idx], vdw_P[:vdw_range_idx], "k--")
ax.plot(vdw_y1[:vdw_range_idx], vdw_P[:vdw_range_idx], "k-")
ax.text(0.45, 0.3e7, "vdW EOS")
# plot Peng-Robinson simulated data
pr_range_idx = 161
ax.plot(x1_sim[:pr_range_idx], pr_P[:pr_range_idx], "k--")
ax.plot(pr_y1[:pr_range_idx], pr_P[:pr_range_idx], "k-")
ax.text(0.65, 1.3e7, "P-R EOS")

# plot settings
ax.set_xlim(0, 1)
ax.set_ylim(0, 200e5)
ax.set_xlabel("$x_1, y_1$")
ax.set_ylabel("$P$ (Pa)")
ax.set_title("Mix of Methane (1) and n-pentane (2) \n at T = 37.78°C")

# custom legend
legend_elements = [
    Line2D([0], [0], marker="x", ls="none", color="k", label="$x_1$ Data"),
    Line2D([0], [0], marker="o", mfc='none', ls="none", color="k", label="$y_1$ Data"),
    Line2D([0], [0], ls="--", color="k", label="$x_1$ EOS"),
    Line2D([0], [0], ls="-", color="k", label="$y_1$ EOS"),
]
ax.legend(handles=legend_elements, bbox_to_anchor=(1, 1))

<matplotlib.legend.Legend at 0x13baed210>

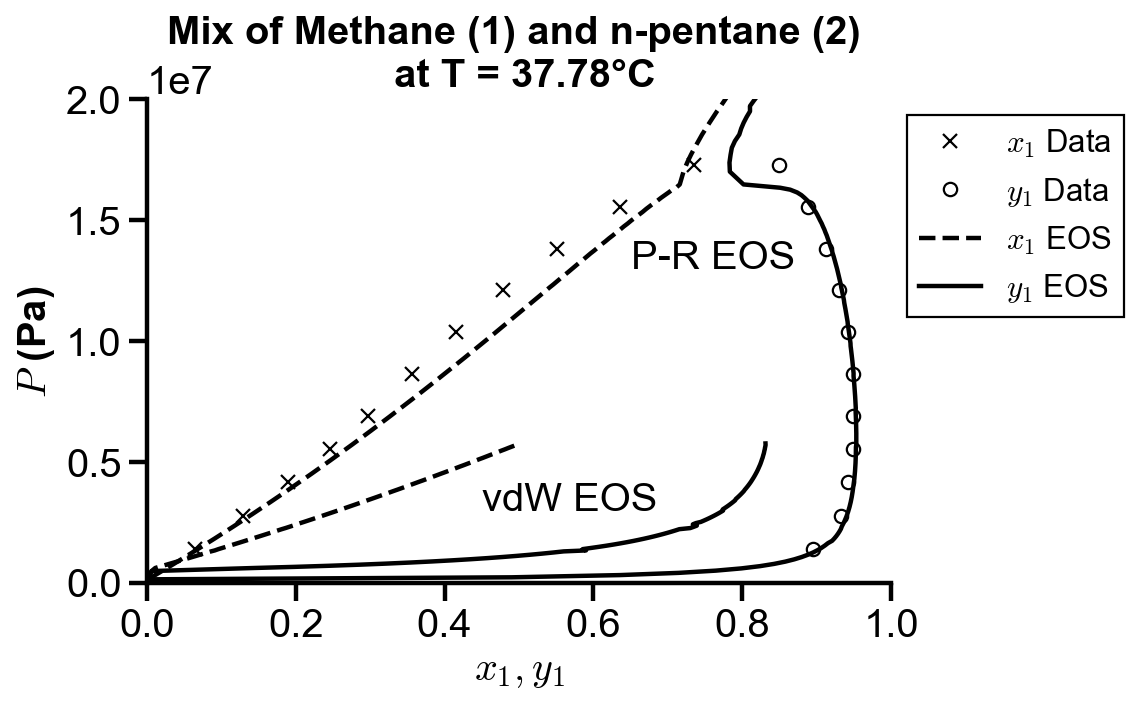
../../_images/55f483f0760bdc6126654123d3de26348220c77e03bdd264e9a8e0fbc9acee60.png

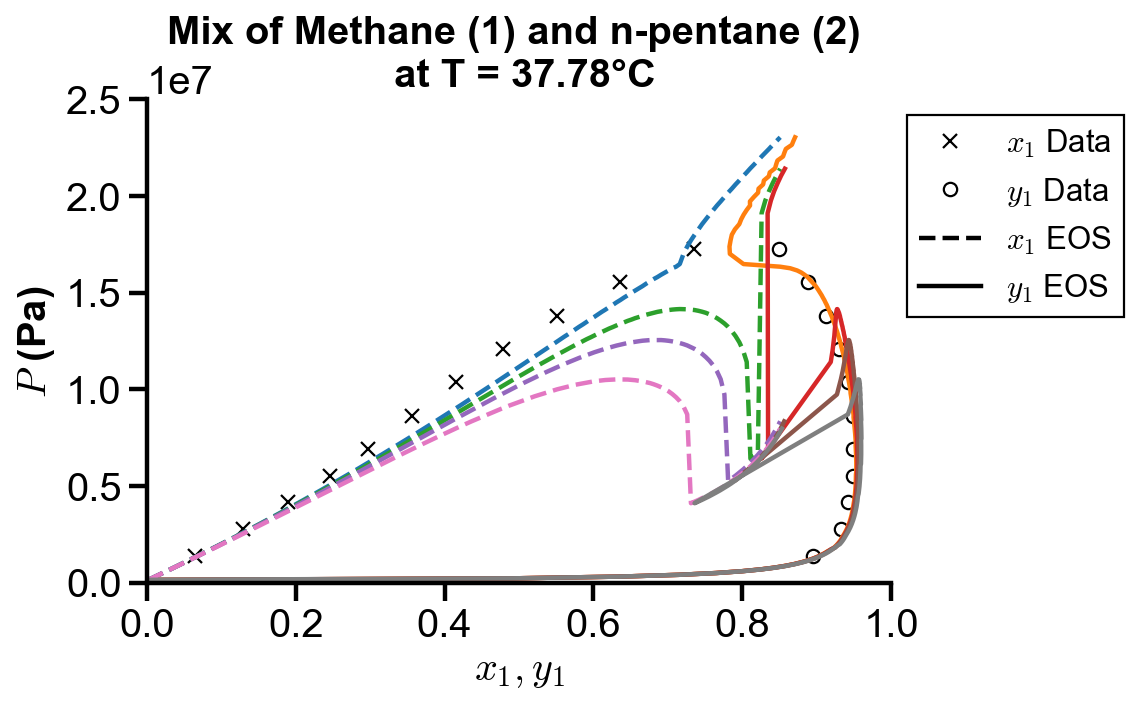
Effect of binary interaction parameter \(k_{12}\) on the Predictions of Peng-Robinson EOS#

Koretsky Example 8.18. Repeat Example 8.17 for the Peng–Robinson equation with values of the binary interaction parameter, \(k_{12}\) of 0.025, 0.05, and 0.10.

# binary interaction parameters to simulate
k12_sim = np.array([0, 0.025, 0.05, 0.1, 1])

# universal constant
R = 8.314  # J/mol K
# given properties
T = 37.78 + 273.15  # K

# formula for Peng-Robinson params and saturation pressure
pure_a = lambda Tc, Pc, R: 0.45724 * (R * Tc) ** 2 / Pc
pure_b = lambda Tc, Pc, R: 0.07780 * (R * Tc) / Pc
kappa = lambda omega: 0.37464 + 1.54226 * omega - 0.26992 * omega**2
alpha = lambda Tr, kappa: (1 + kappa * (1 - np.sqrt(Tr))) ** 2
antoine = lambda A, B, C, T: np.exp(A - B / (T + C)) * 1e5  # Pa

# physical properties - appendix a1
# methane (1)
A1 = 8.6041
B1 = 897.84
C1 = -7.16
omega1 = 0.008
Tc1 = 190.6  # K
Pc1 = 46.00e5  # Pa
Tr1 = T / Tc1
a1 = pure_a(Tc1, Pc1, R)
b1 = pure_b(Tc1, Pc1, R)
kappa1 = kappa(omega1)
alpha1 = alpha(Tr1, kappa1)
a_alpha_1 = a1 * alpha1
# n-pentane (2)
A2 = 9.2131
B2 = 2477.07
C2 = -39.94
omega2 = 0.251
Tc2 = 469.6  # K
Pc2 = 33.74e5  # Pa
Tr2 = T / Tc2
a2 = pure_a(Tc2, Pc2, R)
b2 = pure_b(Tc2, Pc2, R)
kappa2 = kappa(omega2)
alpha2 = alpha(Tr2, kappa2)
a_alpha_2 = a2 * alpha2
# mixture
a12 = np.sqrt(a1 * a2)
a_alpha_12 = np.sqrt(a_alpha_1 * a_alpha_2)

# saturation pressures
Psat1 = antoine(A1, B1, C1, T)
Psat2 = antoine(A2, B2, C2, T)

def solve_v(T, P, a_alpha, b, R, v_before, threshold=1e-10):
    """Solve Peng-Robinson EOS for v."""
    A = a_alpha * P / (R * T) ** 2
    B = b * P / (R * T)
    coeff = [-(A * B - B**2 - B**3), A - 2 * B - 3 * B**2, -(1 - B), 1]
    # solve for compressibility factor
    z = np.polynomial.polynomial.polyroots(coeff)
    # z is real and positive
    z = np.real(z)
    z = z[z > 0]
    # double check if solution is good in case of algorithmic instability
    error = np.abs(np.polynomial.polynomial.polyval(z, coeff))
    z = z[error < threshold]
    # convert to v
    v = z * R * T / P
    v = v[v > b]
    # use the root closest to the last v
    closest_idx = np.argmin(np.abs(v - v_before))
    v = v[closest_idx]
    return v

# formula for mixed Peng-Robinson params
mixed_a_alpha = (
    lambda comp1, comp2, a_alpha_1, a_alpha_2, k12: comp1**2 * a_alpha_1
    + 2 * comp1 * comp2 * np.sqrt(a_alpha_1 * a_alpha_2) * (1 - k12)
    + comp2**2 * a_alpha_2
)
mixed_b = lambda comp1, comp2, b1, b2: comp1 * b1 + comp2 * b2

# formula for fugacity coefficients (phi_1, for phi_2, switch arguments of 1 and 2 properties)
phi = lambda comp1, comp2, P, v, T, R, a_alpha, a_alpha_1, a_alpha_12, b, b1: np.exp(
    b1 / b * (P * v / (R * T) - 1)
    - np.log((v - b) * P / (R * T))
    + a_alpha
    / (2 * np.sqrt(2) * b * R * T)
    * (b1 / b - 2 / a_alpha * (comp1 * a_alpha_1 + comp2 * a_alpha_12))
    * np.log((v + (1 + np.sqrt(2)) * b) / (v + (1 - np.sqrt(2)) * b))
)

pr_P = np.zeros((len(k12_sim), len(x1_sim)))
pr_y1 = np.zeros((len(k12_sim), len(x1_sim)))
pr_y2 = np.zeros((len(k12_sim), len(x1_sim)))
pr_v_v = np.zeros((len(k12_sim), len(x1_sim)))
pr_v_l = np.zeros((len(k12_sim), len(x1_sim)))
pr_phi_v1 = np.zeros((len(k12_sim), len(x1_sim)))
pr_phi_v2 = np.zeros((len(k12_sim), len(x1_sim)))
pr_phi_l1 = np.zeros((len(k12_sim), len(x1_sim)))
pr_phi_l2 = np.zeros((len(k12_sim), len(x1_sim)))

for j in range(len(k12_sim)):
    k12 = k12_sim[j]
    for i in range(len(x1_sim)):
        v_v = 0
        v_l = 0
        # assign current liquid composition
        x1 = x1_sim[i]
        x2 = x2_sim[i]
        # estimate total pressure
        P = x1 * Psat1 + x2 * Psat2
        # estimate vapor compositions
        y1 = x1 * Psat1 / P
        y2 = x2 * Psat2 / P

        # iteratre through Peng-Robinson EOS
        num_iter = 0
        max_iter = 10000
        tol = 0.001
        tol_criteria = tol * 2
        while tol_criteria > tol and num_iter < max_iter:
            # calculate Peng-Robinson parameters for mixtures in each phase
            a_alpha_v = mixed_a_alpha(y1, y2, a_alpha_1, a_alpha_2, k12)
            b_v = mixed_b(y1, y2, b1, b2)
            a_alpha_l = mixed_a_alpha(x1, x2, a_alpha_1, a_alpha_2, k12)
            b_l = mixed_b(x1, x2, b1, b2)
            # print(k12, i, num_iter, a_alpha_v, a_alpha_l)
            # solve Peng-Robinson EOS for molar volume in each phase
            v_v = solve_v(T, P, a_alpha_v, b_v, R, v_before=v_v)
            v_l = solve_v(T, P, a_alpha_l, b_l, R, v_before=v_l)
            # print(i, num_iter, v_v, v_l)
            # calculate fugacity coefficient of each species in each phase
            phi_v1 = phi(y1, y2, P, v_v, T, R, a_alpha_v, a_alpha_1, a_alpha_12, b_v, b1)
            phi_v2 = phi(y2, y1, P, v_v, T, R, a_alpha_v, a_alpha_2, a_alpha_12, b_v, b2)
            phi_l1 = phi(x1, x2, P, v_l, T, R, a_alpha_l, a_alpha_1, a_alpha_12, b_l, b1)
            phi_l2 = phi(x2, x1, P, v_l, T, R, a_alpha_l, a_alpha_2, a_alpha_12, b_l, b2)
            # update vapor composition
            y1 = x1 * phi_l1 / phi_v1
            y2 = x2 * phi_l2 / phi_v2
            # update total pressure
            P = P * (y1 + y2)
            # print(phi_v1, phi_v2, phi_l1, phi_l2)
            # print(y1, y2, P)
            # calculate if calculation converges
            tol_criteria = abs(y1 + y2 - 1)
            num_iter += 1
        # store computed results
        pr_P[j, i] = P
        pr_y1[j, i] = y1
        pr_y2[j, i] = y2
        pr_v_v[j, i] = v_v
        pr_v_l[j, i] = v_l
        pr_phi_v1[j, i] = phi_v1
        pr_phi_v2[j, i] = phi_v2
        pr_phi_l1[j, i] = phi_l1
        pr_phi_l2[j, i] = phi_l2

fig, ax = plt.subplots()

# plot raw data
ax.plot(x1_truth, P_truth, "kx")
ax.plot(y1_truth, P_truth, "ko", mfc="none")
# plot Peng-Robinson simulated data
pr_range_idx = 171 #141
for i in range(4):
    ax.plot(x1_sim[:pr_range_idx], pr_P[i, :pr_range_idx], "--")
    ax.plot(pr_y1[i, :pr_range_idx], pr_P[i, :pr_range_idx], "-")

# plot settings
ax.set_xlim(0, 1)
ax.set_ylim(0, 250e5)
ax.set_xlabel("$x_1, y_1$")
ax.set_ylabel("$P$ (Pa)")
ax.set_title("Mix of Methane (1) and n-pentane (2) \n at T = 37.78°C")

# custom legend
legend_elements = [
    Line2D([0], [0], marker="x", ls="none", color="k", label="$x_1$ Data"),
    Line2D([0], [0], marker="o", ls="none", mfc='none', color="k", label="$y_1$ Data"),
    Line2D([0], [0], ls="--", color="k", label="$x_1$ EOS"),
    Line2D([0], [0], ls="-", color="k", label="$y_1$ EOS"),
]
ax.legend(handles=legend_elements, bbox_to_anchor=(1, 1))

<matplotlib.legend.Legend at 0x13bda52a0>

../../_images/6abd7e4aace2a9e930342fd939a1496871380f3edb3cf0f636d110a8b97e28d2.png

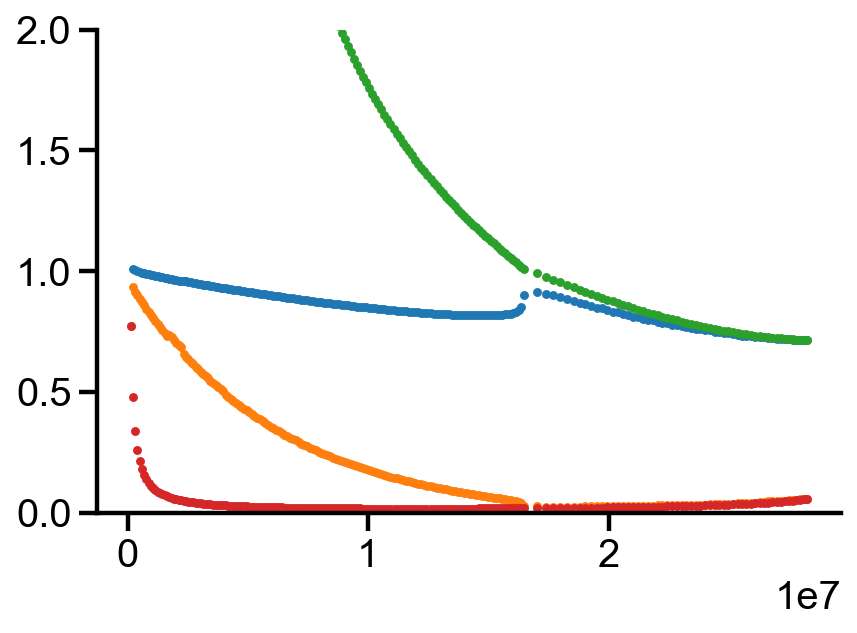
plt.plot(pr_P[0, :], pr_phi_v1[0, :], '.')
plt.plot(pr_P[0, :], pr_phi_v2[0, :], '.')
plt.plot(pr_P[0, :], pr_phi_l1[0, :], '.')
plt.plot(pr_P[0, :], pr_phi_l2[0, :], '.')
plt.ylim(0, 2)

(0.0, 2.0)

../../_images/b9c38dc3b360ebedb7446b800861e0154dd65615bb28597bf0340c020400e3e8.png

pr_v_v[:, 1]

array([0.01152377, 0.01152842, 0.01153307, 0.0115424 , 0.01171438])

k12_sim

array([0.   , 0.025, 0.05 , 0.1  , 1.   ])

pr_P[:, 1]

array([217216.6928621 , 217202.55316504, 217188.36939575, 217159.86883627,
       216614.98058953])

pr_y1[:, 0]

array([0.00100848, 0.00113448, 0.0009912 , 0.0009752 , 0.00100075])