Solving Time-Indepdendent PDEs

Solving Time-Indepdendent PDEs#

Teng-Jui Lin

Content adapted from UW CHEME 375, Chemical Engineering Computer Skills, in Spring 2021.

Python skills and numerical methods
- Finite difference method for PDEs
ChemE applications
- Time-independent 2D heat transfer

Time-independent 2D heat transfer#

Problem Statement. We have a thin metal slab at steady-state, having different temperatures on its four sides. Determine the equilibrium temperature of the slab of points in the interval \([1, 3]\times[1, 3]\) with equal spacing of 1.

Given boundary conditions \(T(0, y) = 75 \mathrm{^\circ C}, T(4, y) = 50 \mathrm{^\circ C}, T(x, 0) = 0 \mathrm{^\circ C}, T(x, 4) = 100 \mathrm{^\circ C}\).

Analytic expression#

Solution. We have the heat transport governing equation

\[ k\nabla^2 T + \dot{q} + \Phi = \rho C_V\dfrac{\partial T}{\partial t} \]

where \(\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\).

Based on the problem statement, we have the assumptions:

No heat source/generation
- \(\dot{q} = 0\)
No fluid or heat movement
- \(\Phi = 0\)
Steady-state system \(\implies\) no time dependence
- \(\frac{\partial T}{\partial t} = 0\)
Thin metal slab \(\implies\) 2D heat transfer (no heat transfer in \(z\) direction)
- \(\frac{\partial^2 T}{\partial z^2} = 0\)
Constant thermal conductivity \(\implies k \not= f(x, y, z, t)\)
- \(k\) can be simplified

Therefore, we can simplify the governing equation:

\[\begin{split} \begin{aligned} k\nabla^2 T + \dot{q} + \Phi &= \rho C_V\dfrac{\partial T}{\partial t} \\ k\nabla^2 T &= 0 \\ \nabla^2 T &= 0 \\ \left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right) T &= 0 \\ \frac{\partial^2T}{\partial x^2} + \frac{\partial^2T}{\partial y^2} &= 0 \end{aligned} \end{split}\]

Numerical approximations#

By central finite difference, we approximate the derivatives by

\[ \dfrac{\partial^2 T}{\partial x^2} \approx \dfrac{T_{i-1, j} - 2T_{i, j} + T_{i+1, j}}{\Delta x^2} \]

\[ \dfrac{\partial^2 T}{\partial y^2} \approx \dfrac{T_{i, j-1} - 2T_{i, j} + T_{i, j+1}}{\Delta y^2} \]

Assume that the spacing in \(x\) and \(y\) directions are the same \(\Delta x = \Delta y = 1\), we have from the original equation:

\[\begin{split} \begin{aligned} \frac{\partial^2T}{\partial x^2} &+& \frac{\partial^2T}{\partial y^2} &= 0 \\ \dfrac{T_{i-1, j} - 2T_{i, j} + T_{i+1, j}}{\Delta x^2} &+& \dfrac{T_{i, j-1} - 2T_{i, j} + T_{i, j+1}}{\Delta y^2} &= 0 \\ T_{i-1, j} - 2T_{i, j} + T_{i+1, j} &+& T_{i, j-1} - 2T_{i, j} + T_{i, j+1} &= 0 \\ \end{aligned} \end{split}\]

For each point in the slab, we write out the expression from the above equation. We also replace the boundary conditions with numerical values. For example, at point \((i, j) = (1, 1)\), we have

\[\begin{split} \begin{aligned} T_{0, 1} - 2T_{1, 1} + T_{2, 1} + T_{1, 0} - 2T_{1, 1} + T_{1, 2} &= 0 \\ T_{0, 1} + T_{1, 0} - 4T_{1, 1} + T_{1, 2} + T_{2, 1} &= 0 \\ - 4T_{1, 1} + T_{1, 2} + T_{2, 1} &= -T_{0, 1} - T_{1, 0} \\ - 4T_{1, 1} + T_{1, 2} + T_{2, 1} &= -75 \\ \end{aligned} \end{split}\]

From PDE to linear algebra#

We can repeat the process for all the points. In this case, we have 9 points, therefore 9 equations and 9 unknowns:

\[\begin{split} \begin{matrix} +4T_{1,1} & -T_{2,1} & & -T_{1,2} & & & & & &=& 75 \\ -T_{1,1} & +4T_{2,1} & -T_{3,1} & & -T_{2,2} & & & & &=& 0 \\ & -T_{2,1} & +4T_{3,1} & & & -T_{3,2} & & & &=& 50 \\ -T_{1,1} & & & +4T_{1,2} & -T_{2,2} & & -T_{1,3} & & &=& 75 \\ & -T_{2,1} & & -T_{1,2} & +4T_{2,2} & -T_{3,2} & & -T_{2,3} & &=& 0 \\ & & -T_{3,1} & & -T_{2,2} & +4T_{3,2} & & & -T_{3,3} &=& 50 \\ & & & -T_{1,2} & & & +4T_{1,3} & -T_{2,3} & &=& 175 \\ & & & & -T_{2,2} & & -T_{1,3} & +4T_{2,3} & -T_{3,3} &=& 100 \\ & & & & & -T_{3,2} & & -T_{2,3} & +4T_{3,3} &=& 150 \\ \end{matrix} \end{split}\]

so we have the system \(\mathbf{A}\mathbf{x} = \mathbf{b}\), where

\[\begin{split} \mathbf{A} = \begin{bmatrix} +4 & -1 & & -1 & & & & & \\ -1 & +4 & -1 & & -1 & & & & \\ & -1 & +4 & & & -1 & & & \\ -1 & & & +4 & -1 & & -1 & & \\ & -1 & & -1 & +4 & -1 & & -1 & \\ & & -1 & & -1 & +4 & & & -1 \\ & & & -1 & & & +4 & -1 & \\ & & & & -1 & & -1 & +4 & -1 \\ & & & & & -1 & & -1 & +4 \\ \end{bmatrix}, \mathbf{x} = \begin{bmatrix} T_{1,1} \\ T_{2,1} \\ T_{3,1} \\ T_{1,2} \\ T_{2,2} \\ T_{3,2} \\ T_{1,3} \\ T_{2,3} \\ T_{3,3} \end{bmatrix}, \mathbf{b} = \begin{bmatrix} 75 \\ 0 \\ 50 \\ 75 \\ 0 \\ 50 \\ 175 \\ 100 \\ 150 \end{bmatrix} \end{split}\]

We can then solve the system of linear equations.

Implementation#

In this approach, we use numpy.linalg.solve() to solve the linear system obtained from simplifying the PDE.

import numpy as np
import matplotlib.pyplot as plt

# create the (sparse) matrix
A_size = 9
A = np.zeros((A_size, A_size))
for i in range(A_size):
    A[i, i] = 4

band_num = 4-1
for i in range(A_size-band_num):
    A[3+i, i] = -1
for i in range(A_size-band_num):
    A[i, 3+i] = -1

band_num = 2-1
for i in range(A_size-band_num):
    A[band_num+i, i] = -1
for i in range(A_size-band_num):
    A[i, band_num+i] = -1
    
for i in range(2, A_size-band_num, 3):
    A[band_num+i, i] = 0
for i in range(2, A_size-band_num, 3):
    A[i, band_num+i] = 0
A

array([[ 4., -1.,  0., -1.,  0.,  0.,  0.,  0.,  0.],
       [-1.,  4., -1.,  0., -1.,  0.,  0.,  0.,  0.],
       [ 0., -1.,  4.,  0.,  0., -1.,  0.,  0.,  0.],
       [-1.,  0.,  0.,  4., -1.,  0., -1.,  0.,  0.],
       [ 0., -1.,  0., -1.,  4., -1.,  0., -1.,  0.],
       [ 0.,  0., -1.,  0., -1.,  4.,  0.,  0., -1.],
       [ 0.,  0.,  0., -1.,  0.,  0.,  4., -1.,  0.],
       [ 0.,  0.,  0.,  0., -1.,  0., -1.,  4., -1.],
       [ 0.,  0.,  0.,  0.,  0., -1.,  0., -1.,  4.]])

b = np.array([75, 0, 50, 75, 0, 50, 175, 100, 150])

temperatures = np.linalg.solve(A, b)
temperatures

array([42.85714286, 33.25892857, 33.92857143, 63.16964286, 56.25      ,
       52.45535714, 78.57142857, 76.11607143, 69.64285714])

row = 3
col = 3
T_profile = temperatures.reshape(row, col)

for i in np.arange(6, -1, -3):
    print('{:.2f} | {:.2f} | {:.2f}'.format(*temperatures[i:i+3]))

57 | 76.12 | 69.64
17 | 56.25 | 52.46
86 | 33.26 | 33.93

Plotting annotated heatmap#

# plot settings
%config InlineBackend.figure_format = 'retina'
%matplotlib inline

plt.rcParams.update({
    'font.family': 'Arial',  # Times New Roman, Calibri
    'font.weight': 'normal',
    'mathtext.fontset': 'cm',
    'font.size': 18,
    
    'lines.linewidth': 2,
    
    'axes.linewidth': 2,
    'axes.spines.top': False,
    'axes.spines.right': False,
    'axes.titleweight': 'bold',
    'axes.titlesize': 18,
    'axes.labelweight': 'bold',
    
    'xtick.major.size': 8,
    'xtick.major.width': 2,
    'ytick.major.size': 8,
    'ytick.major.width': 2,
    
    'figure.dpi': 80,
    
    'legend.framealpha': 1, 
    'legend.edgecolor': 'black',
    'legend.fancybox': False,
    'legend.fontsize': 14
})

import seaborn as sns
T_heatmap = sns.heatmap(T_profile, square=True, cbar=True,
                        annot=True, fmt=".1f", cmap='Reds',
                        cbar_kws={'label': '$T \ [^\circ C]$', 
                                  'format': '%i', 
                                  'ticks': np.linspace(temperatures.min(), temperatures.max(), 5)})
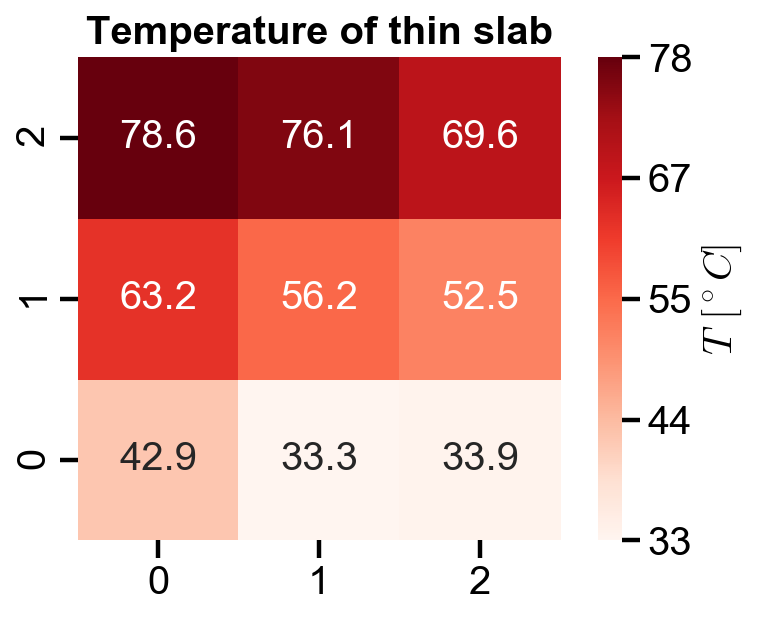
T_heatmap.set_title('Temperature of thin slab')
T_heatmap.invert_yaxis()

../../_images/85b00d4bfa00903acf4d4dd0397eb104813356858597b4f0837d1bb5c012e52f.png